Solution
It is given that the width of a rectangle is 2 inches longer than the height.
If the height is h inches,
The width of the rectangle is (2 + h) inches
If the diagonal measurement is 58 inches.
Using Pythagoras theorem, the relationship between the three sides is given as
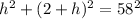
Expanding the brackets;
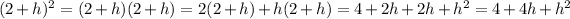
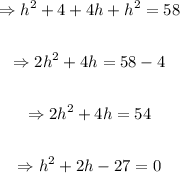
Using the quadratic formula,
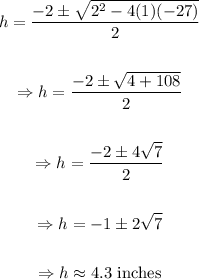
Hence, the height is 4.3 inches