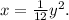Question

Driving equation of a parabola giving its focus and Directrix

Answer 1

a) Notice that Q is on the line x=-3, then the x-coordinate of Q is -3.

Since Q and P(x,y) are in the same horizontal line, then they must have the same y-coordinate, therefore:

`Q=(-3,y).`

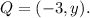
b) Recall that the length of a segment is the distance between its terminal points, then:

`\begin{gathered} FP=√((x-3)^2+(y-0)^2)=√((x-3)^2+y^2), \\ QP=√((x+3)^2+(y-y)^2)=√((x+3)^2), \\ since\text{ }x>-3,\text{ }QP=x+3. \end{gathered}`

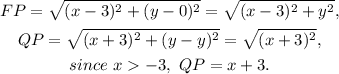
c) Recall that a parabola is a curve where any point is at an equal distance from a fixed point (the focus) and a fixed straight line (the directrix), then:

`FP=QP.`

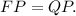
d) Substituting FP and QP we get:

`x+3=√((x-3)^2+y^2)^.`

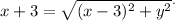
Therefore:

`\begin{gathered} (x+3)^2=(x-3)^2+y^2, \\ x^2+6x+9=x^2-6x+9+y^2, \\ 12x=y^2, \\ x=(1)/(12)y^2. \end{gathered}`

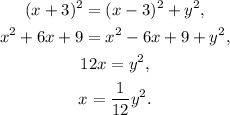
Answer:

(a) (-3,y)

(b)

`\begin{gathered} FP=√((x-3)^2+y^2), \\ QP=x+3. \end{gathered}`

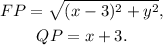
(c)

`FP=QP.`

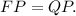
(d)

`x=(1)/(12)y^2.`