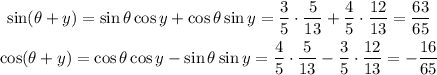In a right triangle, we haev some trigonometric relationships between the sides and angles. Given an angle, the ratio between the opposite side to the angle by the hypotenuse is the sine of this angle, therefore, the following statement
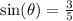
Describes the following triangle
To find the missing length x, we could use the Pythagorean Theorem. The sum of the squares of the legs is equal to the square of the hypotenuse. From this, we have the following equation
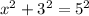
Solving for x, we have
![\begin{gathered} x^2+3^2=5^2 \\ x^2+9=25 \\ x^2=25-9 \\ x^2=16 \\ x=\sqrt[]{16} \\ x=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/5kxencf5cj3ky4z6z7qdg415m5b1sgxnzi.png)
The missing length of the first triangle is equal to 4.
For the other triangle, instead of a sine we have a tangent relation. Given an angle in a right triangle, its tanget is equal to the ratio between the opposite side and adjacent side.The following expression
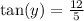
Describes the following triangle
Using the Pythagorean Theorem again, we have
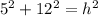
Solving for h, we have
![\begin{gathered} 5^2+12^2=h^2 \\ 25+144=h^2 \\ 169=h^2 \\ h=\sqrt[]{169} \\ h=13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ybc9i5icclkiates62t9t95dy7m1q7am8o.png)
The missing side measure is equal to 13.
Now that we have all sides of both triangles, we can construct any trigonometric relation for those angles.
The sine is the ratio between the opposite side and the hypotenuse, and the cosine is the ratio between the adjacent side and the hypotenuse, therefore, we have the following relations for our angles
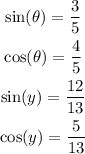
To calculate the sine and cosine of the sum
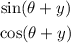
We can use the following identities
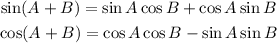
Using those identities in our problem, we're going to have