Given the compound interest formula:
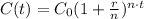
Where C₀ is the initial amount in the account, r is the interest rate, and n is the number of times the interest is compounded in one year. From the problem, we identify:
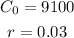
Additionally, there are 52 weeks in a year, so if the interest is compounded weekly:

Using these values in the equation:

If the money is left for 5 years, then t = 5, so the amount of money after 5 years is:
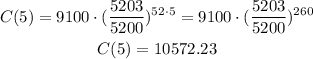
There are $10,572.23 in the bank account after 5 years.