Question

2 STEP PROBLEM:STEP 1:Completely factor the left-hand side of the equation into two or more factors: 81x^4 - 64x^2 = 0STEP 2:Solve the given equation by factoring. Write your answer in reduced fraction form, if necessary. Separate multiple solutions with a comma. 81x^4 - 64x^2 = 0

Answer 1

We want to factor the equation

`81x^4-64x^2=0`

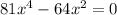
But this is a difference of 2 squares problem, since

`81x^4=(9x^2)^2`

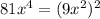
and

`64x^2=(8x)^2`

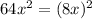
Thus,

`\begin{gathered} 81x^4-64x^2=(9x^2)^2-(8x)^2 \\ =(9x^2-8x)(9x^2+8x)=0 \end{gathered}`

This can further be factorized as,

`(x)(x)(9x-8)(9x+8)`

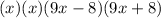
This is the solution to STEP 1, as you can see, there are 4 factors.

2. We want to get the solutions from this factored form, i.e the values of x that makes

`(x)(x)(9x-8)(9x+8)=0`

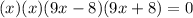
We see that this happens, when x = 0 twice, and when

`\begin{gathered} 9x-8=0 \\ 9x=8 \\ x=(8)/(9) \end{gathered}`

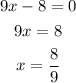
also when,

`\begin{gathered} 9x+8=0 \\ 9x=-8 \\ x=-(8)/(9) \end{gathered}`

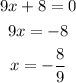
Therefore the solutions are

`0,0,(8)/(9),-(8)/(9)`

This is the answer to Part B