ANSWER
Not a proportional relationship
Step-by-step explanation
For this to be a proportional relationship the ratio y:x for each pair of the table must be constant:
For the first pair:
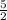
Second pair:
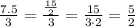
Third pair:
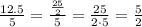
Until now the ratio is constant, but for the fourth pair:
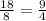
The ratio is different. Therefore, the relation between x and y in the table is not proportional.