Question

Graph the following system of inequalities on the coordinate plane. You will need to explain your work.

Answer 1

To graph the inequality:

`4x+5y\leq20`

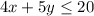
we first write it like an equation:

`4x+5y=20`

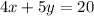
Now, we know that a linear equation always represent a line; to graph we it we need to points; the easiest points to get are the x and y intercept.

The x-intercept happens when y=0, from the equation we have:

`\begin{gathered} 4x=20 \\ x=(20)/(4) \\ x=5 \end{gathered}`

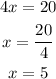
then we have the point (5,0)

The y-intercept happens when x=0, from the equation we have:

`\begin{gathered} 5y=20 \\ y=(20)/(5) \\ y=4 \end{gathered}`

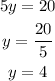
then we have the point (0,4)

Now that we have two points we plot them on the plane and join them with a solid straight line, we need to do this since the inequality is not a strict one:

Finally we need to decide which area to shade to do this we notice that the sign on the inequality is a less or equal to, this means that we have to shade the area below the line, therefore the graph of the inequality is:

To graph the second inequality:

`y>-4`

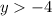
we write it like an equation:

`y=-4`

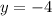
Now we know that this is an horizontal lines that intersects the y-axis at -4, therefore we draw a dashed line at this height on the plane, we need to use a dashed line since this is a strict inequality:

Finally we need to determine what region to shade, since the inequality express that y has to be greater than -4 then we shade the upper part, therefore the graph of the inequality is: