The cost function has a fixed part ($40,000) and a variable part, that depends on the number of CD's (14x), so we can write the cost function as:
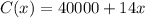
The revenue is equal to the unit price times the number of CD's:

The profit function is the difference between the revenue and the cost:
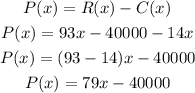
The number of CD's that must be produced and sold to breakeven happens when C(x)=R(x) or P(x)=0, so we can write:
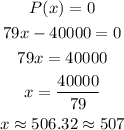
Answer:
C = $40000 - $14x
R = $93x
P = $79x - $40000
The breakeven number of CD's is 507 units.