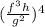First part
numerator f cubed g to the power of negative 2
The numerator can be written as
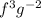
Second part
denorminator h raised to the power of negative 1
The numerator can be written as
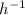
combining part one and two
Open parentheses fraction - fraction - close parentheses to the power of 4
This gives
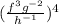
simplifying the expression to remove negative exponent
Simplifying the numerator
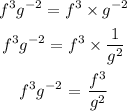
simplfying the denorminator
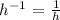
combining simplfied values for numerator and denorminator in the general form we have
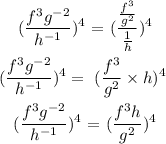
Hence, the simplified form of the expression is