Question

On a treasure map with coordinates, James is standing on the point (-9, -1). He knows that a treasure chest is located 10 units away from where he is standing and that the coordinates of the treasure chest are such that the x-coordinate is six less than the y-coordinate. Determine and state the possible location(s) of the treasure chest using the Pythagorean Theorem.

Answer 1

According to the given information, the coordinates of the treasure chest are related this way:

`x=y-6`

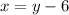
We also know that James is 10 units away from the treasure chest, it means this is the distance between the 2 points. We can use this information and pythagorean theorem to find the possible locations of the treasure chest:

`\begin{gathered} d=\sqrt[]{(x-(-9))^2+(y-(-1))^2} \\ d=\sqrt[]{((y-6)+9)^2+(y+1)^2} \\ d=\sqrt[]{(y+3)^2+(y+1)^2} \\ d=\sqrt[]{y^2+6y+9+y^2+2y+1} \\ d^2=y^2+6y+9+y^2+2y+1 \\ 10^2=2y^2+8y+10 \\ 100=2y^2+8y+10 \\ 0=2y^2+8y-90 \\ 0=y^2+4y-45 \\ 0=(y+9)(y-5) \\ 0=y+9 \\ y1=-9 \\ 0=y-5 \\ y2=5 \end{gathered}`

It means that the y coordinates can be -9 or 5. We can use these values of y to find x using the relation given at the beginning:

`\begin{gathered} x=y-6 \\ x1=-9-6 \\ x1=-15 \\ x2=5-6 \\ x2=-1 \end{gathered}`

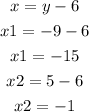
It means that the possible locations of the treasure chest are (-15,-9) or (-1,5)