Question

Explain how you can tell whether an even number can be written a the sum of three consecutive whole numbers .

Answer 1

ASSUMPTIONS:

1) Let the even number be n.

2) Let the second of the 3 consecutive numbers be x. Therefore, we have the 3 consecutive numbers to be:

`(x-1),x,(x+1)`

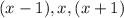
PROOF:

We have that:

`n=(x-1)+x+(x+1)`

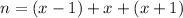
Solving the right-hand side:

`\begin{gathered} n=x-1+x+x+1 \\ n=3x \end{gathered}`

Since n is even, that means that x must be even.

We can get the value of x to by dividing both sides by 3 to get:

`x=(n)/(3)`

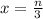
Since x is an even whole number, n must be divisible by 3.

CHECK:

Try n = 18:

`\begin{gathered} x=(18)/(3) \\ x=6 \end{gathered}`

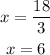
Hence, the 3 numbers will be:

`\begin{gathered} (6-1),6,(6+1) \\ \Rightarrow5,6,7 \end{gathered}`

The sum is:

`5+6+7=18`

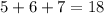
This proves the theory.

CONCLUSION:

For an even number to be able to be written as the sum of three consecutive whole numbers, it has to be DIVISIBLE BY 3.