Question

A gentleman is losing 26% of his hair each year. If he currently has 1,889hairs on his head, about how many hairs will he have left after 8 years? *

Answer 1

This situation follows the next exponential decay formula:

`y=a(1+r)^t`

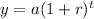
where

• a is the initial hairs

,

• r is the losing rate (as a decimal)

,

• t is time in years

,

• y is the remaining hairs

Replacing with a = 1889, r = -0.26 (notice the negative sign) and t = 8, we get:

`\begin{gathered} y=1889(1-0.26)^8 \\ y=1889(0.74)^8 \\ y\approx170 \end{gathered}`

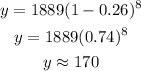
He will have left about 170 hairs after 8 years