Question

Write the equation of a quadratic function that has x-intercepts at (2,0) and (-3,0)

Answer 1

y = x² + x - 6

Step-by-step explanation:

A quadratic function with x-intercepts in (a, 0) and (b, 0) has the form:

`y=(x-a)(x-b)`

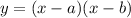
Therefore, the equation of a quadratic function that has x-intercepts at (2, 0) and (-3, 0) is:

`\begin{gathered} y=(x-2)(x-(-3)) \\ y=(x-2)(x+3) \end{gathered}`

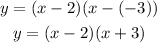
Finally, we can apply the distributive property to get:

`\begin{gathered} y=(x\cdot x)+(x\cdot3)-(2\cdot x)-(2_{}\cdot3) \\ y=x^2+3x-2x-6 \\ y=x^2+x-6 \end{gathered}`

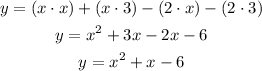
So, the answer is:

y = x² + x - 6