Question

The pressure in the metal tube is 120 000 N/m2 at 300 K. a pressure of 180 000 N/m2 to activate the alarm. Apply equations in order to solve and calculate the minimum temperature, in K at which the alarm is activated.

Answer 1

Given,

The initial pressure of the gas, P₁=120000 N/m²

The initial temperature of the gas, T₁=300 K

The required pressure of the gas, P₂=180000 N/m²

From Gay-Lussac's law,

`(P_1)/(T_1)=(P_2)/(T_2)`

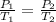
Where T₂ is the required teperature to achieve the given gas pressure.

On substituting the known values,

`\begin{gathered} (120000)/(300)=(180000)/(T_2) \\ \Rightarrow T_2=(180000*300)/(120000) \\ =450\text{ K} \end{gathered}`

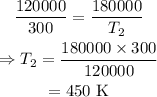
Thus the alarm is activated at the temperature of 450 K

(i)

When the temperature of the gas is increased the kinetic energy of the molecules of the gas increases. This results in increased collision between the molecules. Increased collision causes the pressure of the gas to increase. Due to this pressure, the piston is pushed and the alarm goes off.