We are given that a line passes through the points (1, -2) and (4, -2)
Recall that the equation of the line in slope-intercept form is given by

Where m is the slope and b is the y-intercept.
The slope of the line is given by
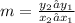
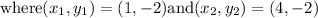
Let us substitute the given values into the slope formula
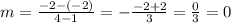
So the slope is 0 (check option 1)
Now let us find the y-intercept (b)
Choose any one point from the given two points
Let choose (1, -2) and substitute it into the slope-intercept equation
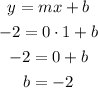
So the y-intercept is -2 (check option 2)
The equation of the line becomes
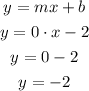
So the equation of the line is y = -2 (check option 6)
Also note that horizontal lines have 0 slope.
Since the slope is 0, it is a horizontal line (check option 4)
Conclusion:
Options 1, 2, 4 and 6 are correct.