Composition of inverse functions:
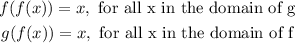
For the given functions:
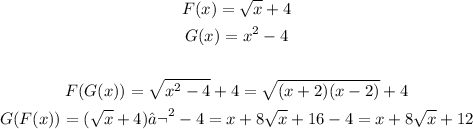
As you can see above the compossition of the given functions is not equal to x, then the given functions are not inverse
Answer: A. No, because the composition does not result in an answer of x.