Question

- matrices-find the x and y so that.. (see image)

Answer 1

So we want to find x and y so that:

For this, we have to remember that both matrices have equal components.

So we could equal:

`\begin{gathered} x+3=4 \\ y=2x+2 \end{gathered}`

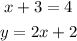
We could solve the first equation:

`\begin{gathered} x+3=4 \\ x=4-3 \\ x=1 \end{gathered}`

And, as we know that x=1, we could replace this value in the expression:

`\begin{gathered} y=2x+2 \\ y=2\cdot1+2 \\ y=2+2 \\ y=4 \end{gathered}`

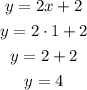
And these are the values for x and y.