In the uppermost angle labelled with angles 20 and 80, the third angle which is angle d equals 80.

Where you have the angle labelled 65 degree, the angle right beside it equals 115 degrees. Angles on a straight line sum up to 180 degrees, therefore, the unlabelled angle beside 65 lies along the same line segment and that makes it equal to 115. Observe also that in the triangle which contains angle 20 degrees, you have angle b and the other one we just derived which is angle 115. This means in that triangle, we now have,
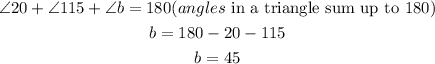
Observe that in the right angled triangle, the other two angles are marked with just one curve, which indicates that both are congruent (angle a and the other one that lies between h and 80). If both are congruent, then it means the triangle is made up of 90 degrees and two other angles that are equal in measure. Lets call the other angle a2. Hence;
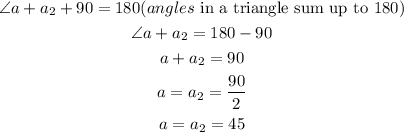
Observe that angles 80, a2 and h all lie on the same straight line.
Hence;
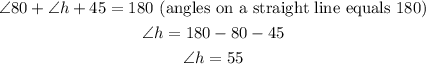
In the triangle that contains angles 95 and h (which we have derived as 55 degrees), the third angle to the left is calculated as follows (we shall call the unlabelled angle x)
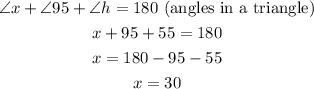
In the triangle that contains angle 65, angle a and angle f, angle a has been derived as 45. Therefore

Note that angle f plus angle g equals 90 degrees. Therefore angle g is derived as;

Observe also that the angle labelled c lies in a large triangle which has two congruent angles indicated by the double curves. That means the othe angle at the bottom right measures the same as angle c. The third angle in this triangle comprises of two angles which are angles g (which is 20 degrees) and the one we labelled as x (which we derived as 30 degrees). Therefore the third angle is g plus x, which is 20 plus 30 which equals 50.
Hence;
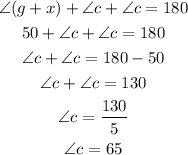
In the triangle labelled with angle e, one of the angles has been derived as 65, while the other one on the left beside (angle 95) is derived as 85. Reason is angles on a straight line equals 180, that is, unknown angle plus 95 equals 180. This means the bottom right triangle has angles 85, 65 and e. Therefore;
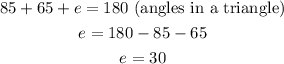
The labelled angles therefore are;
a = 45
b = 45
c = 65
d = 80
e = 30
f = 70
g = 20 and
h = 55