Question

Each student at the State University has a student ID number consisting of six digits (the first digit is non zero and the digits can repeat) followed by two letters A, B, C, D, and E (letters cannot repeat). How many different student numbers are possible?

Answer 1

For the first part of the ID number (consisting of digits) we have the following number of permutations

`9\cdot10\cdot10\cdot10\cdot10\cdot10`

The first part 9 takes into consideration that the first digit is non-zero, so we only have 1-9 to choose from, while the other succeeding 5 digits we have 10 to choose from (0 - 9).

The second part of the ID number (two letter part) will have the number of permutations

`5\cdot4`

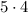
First multiplied by 5, and then 4, since we cannot repeat the previous letter.

Therefore the number of different student numbers is solved as

`9\cdot10\cdot10\cdot10\cdot10\cdot10\cdot5\cdot4=18,000,000`

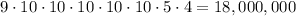
18,000,000 possible student ID numbers.