Question

A system of linear equations is given by the tablesThe first equation of this system is y = x + 3.The second equation of this system is y = 3x − .The solution of the system is

Answer 1

Step 1

The first equation of this system

y = mx + c

c is the intercept on the y-axis.

`\begin{gathered} c\text{ = 3} \\ m\text{ = }\frac{Rise\text{ in y}}{Rise\text{ in x}} \\ m\text{ = }(3-1)/(0-(-1))\text{ = }(2)/(1)\text{ = 2} \end{gathered}`

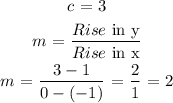
The first equation of this system is y = 2x + 3.

Step 2:

`\begin{gathered} c\text{ = -1} \\ m\text{ = }\frac{11\text{ - 5}}{4\text{ - 2}} \\ m\text{ = }(6)/(2)\text{ = 3} \end{gathered}`

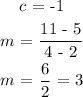
The second equation of this system is y = 3x - 1.

Step 3:

Solve both systems of equations:

`\begin{gathered} y\text{ = 2x + 3} \\ y\text{ = 3x - 1} \\ 3x\text{ - 1 = 2x + 3} \\ 3x\text{ - 2x = 3 + 1} \\ x\text{ = 4} \\ y\text{ = 3x - 1} \\ y\text{ = 3}*4\text{ - 1} \\ y\text{ = 12 - 1} \\ y\text{ = 11} \end{gathered}`

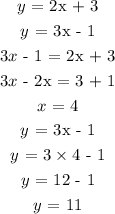
The solution of the system is (4, 11)