The area of the mean for a unformly distribution is gievn below
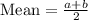
Given that a is the minimum or lowest value and b is the maximum or highest value
From the question given,
a= 0; b=4.1
The mean of this distribution is as shown below
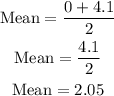
Hence the mean of this distribution is 2.05
The standard deviation of the uniformly distribution is given by the formula below:
![s_d=\sqrt[]{((b-a)^2)/(12)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/7c607auiyakpdc17l42ca1jldce7d01mpj.png)
The standard deviation is as shown below:
![\begin{gathered} s_d=\sqrt[]{((4.1-0)^2)/(12)} \\ s_d=\sqrt[]{(4.1^2)/(12)} \\ s_d=\sqrt[]{(16.81)/(12)} \\ s_d=\sqrt[]{1.400833} \\ s_d=1.183568 \\ s_d=1.1836(\text{correct to 4 decimal place)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/99ieaxmtcor4dslph6qr4hoykcvwp3wg89.png)
Hence, the standard deviation is 1.1836 to the nearest 4 decimal place
The probability of exactly 2.6 is 0. This is because the probability of finding an exact number of a uniform distribution is 0
c. The probability that the round off error for a jumper's distance is exactly 2.6 is
P(x = 2.6) = 0
The probability that the round off error for the distance that a long jumper has jumped is
between 0.7 and 1.2 mm P(0.7 <3 <1.2) is as shown below:
![\begin{gathered} P(0.7<strong>d. Hence, probability that the round off error for the distance that a long jumper has jumped is</strong><p><strong>between 0.7 and 1.2 mm P(0.7 <3 <1.2) is 0.1220 correct to four decimal place</strong></p><p>The probability that the jump's round off error is greater than 2.72 is P(x > 2.72). This can be solved as shown below</p>[tex]\begin{gathered} P(x>2.72)=(4.1-2.72)((1)/(4.1-0)) \\ =1.38*(1)/(4.1) \\ =1.38*0.2439024 \\ =0.336585\approx0.3366(nearrest\text{ 4 decimal place)} \end{gathered}]()
e. Hence, the probability that the jump's round off error is greater than 2.72 is P(x > 2.72) = 0.3366
P(x > 1.7 x > 0.7) is as shown below:

f. Hence, P(x > 1.7 / x > 0.7) = 0.7059 correct to 4 decimal place
The 43rd percentile is

g. Hence, the 43rd percile is 1.763
The minimum for the upper quarter is as shown below
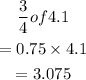
h. Hence, the minimum for the upper quarter is 3.075