Question

I’m sure I have the right answer i just need to know how I got here or maybe I don’t have the write answer

Answer 1

To find the points at which the tangent line is horizontal, it is enough to find where the slope of the function is 0 because a horizontal line's slope is 0.

Find f'(x).

`f^(\prime)(x)=3x^2-9`

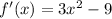
Now set it equal to 0 and solve for x to find the x values at which the tangent line is horizontal to given function.

`\begin{gathered} 3x^2-9=0 \\ 3x^2=9 \\ x^2=3 \\ x=\pm\sqrt[]{3} \end{gathered}`

Find the function values at these x-values.

`\begin{gathered} f(\sqrt[]{3})=(\sqrt[]{3})^3-9\sqrt[]{3} \\ =3\sqrt[]{3}-9\sqrt[]{3} \\ =3\sqrt[]{3}(1-3) \\ =-6\sqrt[]{3} \end{gathered}`

`\begin{gathered} f(-\sqrt[]{3})=(-\sqrt[]{3})^3+9\sqrt[]{3} \\ =-3\sqrt[]{3}+9\sqrt[]{3} \\ =3\sqrt[]{3}(-1+3) \\ =6\sqrt[]{3} \end{gathered}`

The points where the graph of the function have horizontal tangents are

`(\sqrt[]{3},-6\sqrt[]{3}),(-\sqrt[]{3},6\sqrt[]{3})`

Option A is correct.