Answer:
A = 2298.48
Explanation:
The right triangle with the 35angle. you need to find the height of that triangle which is the adjacent side and the opposite side is 44
tan 35° = opposite/ adjacent

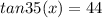
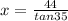
x = 62.83 ≈ 62.8
Using the 25° angle, you have the height which is 62.8 and looking for the side opposite the 25° angle.
So tan 23° = x/adjacent side
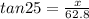
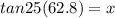
29.28 ≈29.2 A = 1/2bh ; A = 1/2 (44 + 29.2)(62.8) ; A = 2298.48