Question

1. Describe and extend each sequence. A. The height, in feet, of windowsills in a high-rise building is represented by this sequence: 3, 15, 27, 39, ... Describe the rule for the sequence. Find the next two terms of the sequence. Show your work. B. Mason put sticky notes on some pages of his math book. The page numbers form this sequence: 3,5,8,13, 21, 34, ... Describe the rule for the sequence.

Answer 1

A.

The first sequence is

3, 15, 27, 39, ....

we notice that in this sequence the difference between each number is always the same, in this case 12. In the case where the difference is the same in each term we can use the following formula for the nth term

`dn+(a-d)`

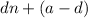
where n represents the nth term, d is the difference and a is the first term in the sequence, in our case we will have

`12n+(3-12)`

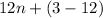
Therefore the rule for the sequence is

`12n-9`

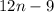
the next two term in the sequence are the fifth and sixth. Then

`\begin{gathered} \text{fifth term}\rightarrow51 \\ sixth\text{ term}\rightarrow63 \end{gathered}`

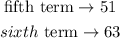
Another way to write the nth term in a sequence where the diference between each term is the same is using the formula

`\begin{gathered} a_n=a_(n-1)+d \\ \text{where } \\ a_n\text{ }\rightarrow\text{is the nth term} \\ a^{}_(n-1)_{}\rightarrow is\text{ the (n-1)th term } \\ d\rightarrow is\text{ the difference betw}en\text{ each term} \end{gathered}`

In this case we have that

`\begin{gathered} a_1=3 \\ a_2=15 \\ a_3=27 \\ a_4=39 \end{gathered}`

Now we have to notice that we start with three and the the second term has to be 12 more in each term this means that the term should be multiply by 12. In general the nth term will be of the form

`12n`

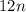
But this doesn't work for our case since we don't start at twelve, so we have to substract the appropiate amount to find the first term.

`a_n=12n-9`

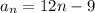
B.

This sequence is almost the Fibonacci sequence but it doesn't start in 1.

The only way to describe this sequence is by the following recursively definition

`\begin{gathered} a_n=a_(n-1)+a_{n-2\text{ }} \\ \text{for n>}3 \end{gathered}`

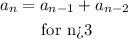
where

`\begin{gathered} a_1=3 \\ a_2=5 \\ a_3=8 \end{gathered}`

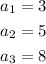
This means that the nth term is the sum of the two preceding terms.

The next two terms of the sequence are:

`\begin{gathered} a_7=a_6+a_5=34+21=55 \\ a_8=a_7+a_6=55+34=89 \end{gathered}`

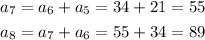
I will finish the session, but the answer will be in you account. Have a great night