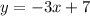Write an equation for the line parallel to the given line that contains CC(1,4); y=-3x+8y=(type your answer in slope-intercept form)

Question

asked Feb 9, 2023 23.8k views

1 Answer

Qaswed · Answer 1 · 2023-02-14T03:54:22+0000

Answer:

The equation of the line is:

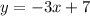
Step-by-step explanation:

Given that the line is parallel to the line;

And passes through the point;

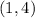
Since the line is parallel to the given equation, they must have the same slope.

So, the slope of the line is -3;

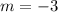
We now need to calculate the y intercept b of the line;

substituting the slope and the given point;

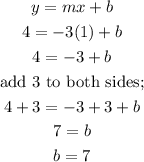
$\begin{gathered} y=mx+b \\ 4=-3(1)+b \\ 4=-3+b \\ \text{add 3 to both sides;} \\ 4+3=-3+3+b \\ 7=b \\ b=7 \end{gathered}$

Therefore, the equation of the line is;