To answer this question, we need to use the binomial theorem, and we have the identity when we raise the binomial to 4:
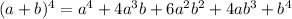
And we also have that:
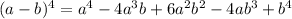
And now, we know that the values for a and b are:
![a=\sqrt[]{5},b=\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/drlblp4emht7q6vah42uiz6bv24wuiec8x.png)
Then, we also know that we need the result for:
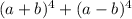
Then, if we substitute the equivalent expressions, we have:
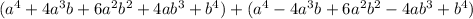
Simplifying, we have - we need to add the like terms as follows:
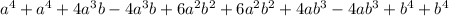
Therefore:
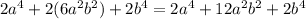
We see that some terms were canceled since they are the same with opposite signs:
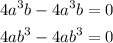
Now, we can substitute the values for a and b as follows:
![a=\sqrt[]{5},b=\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/drlblp4emht7q6vah42uiz6bv24wuiec8x.png)
We need to remember that:
![\sqrt[]{5}=5^{(1)/(2)},\sqrt[]{2}=2^{(1)/(2)}](https://img.qammunity.org/2023/formulas/mathematics/college/sjyfqkduy6xwj9jvcc1oqxkl6ly4ej3r9h.png)
Then we have:
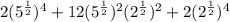
Thus
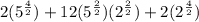
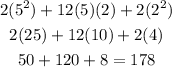
In summary, therefore, we have that:
![(\sqrt[]{5}+\sqrt[]{2})^4+(\sqrt[]{5}-\sqrt[]{2})^4=178](https://img.qammunity.org/2023/formulas/mathematics/college/x1d4g24y3tqogl05vvlya348ox7nj10i7c.png)