Question

Can you help me with questions no 13 only part b

Answer 1

To answer this question, we need to use the binomial theorem, and we have the identity when we raise the binomial to 4:

`(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4`

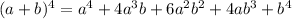
And we also have that:

`(a-b)^4=a^4-4a^3b_{}+6a^2b^2-4ab^3+b^4`

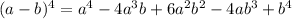
And now, we know that the values for a and b are:

`a=\sqrt[]{5},b=\sqrt[]{2}`

Then, we also know that we need the result for:

`(a+b)^4+(a-b)^4`

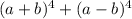
Then, if we substitute the equivalent expressions, we have:

`(a^4+4a^3b+6a^2b^2+4ab^3+b^4)+(a^4-4a^3b_{}+6a^2b^2-4ab^3+b^4)`

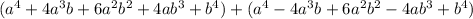
Simplifying, we have - we need to add the like terms as follows:

`a^4+a^4+4a^3b-4a^3b+6a^2b^2+6a^2b^2+4ab^3-4ab^3+b^4+b^4`

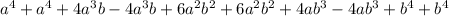
Therefore:

`2a^4+2(6a^2b^2)+2b^4=2a^4+12a^2b^2+2b^4`

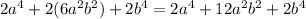
We see that some terms were canceled since they are the same with opposite signs:

`\begin{gathered} 4a^3b-4a^3b=0 \\ 4ab^3-4ab^3=0 \end{gathered}`

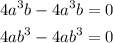
Now, we can substitute the values for a and b as follows:

`a=\sqrt[]{5},b=\sqrt[]{2}`

We need to remember that:

`\sqrt[]{5}=5^{(1)/(2)},\sqrt[]{2}=2^{(1)/(2)}`

Then we have:

`2(5^{(1)/(2)})^4+12(5^{(1)/(2)})^2(2^{(1)/(2)})^2+2(2^{(1)/(2)})^4`

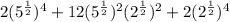
Thus

`2(5^{(4)/(2)})+12(5^{(2)/(2)})(2^{(2)/(2)})+2(2^{(4)/(2)})`
`\begin{gathered} 2(5^2)+12(5)(2)+2(2^2) \\ 2(25)+12(10)+2(4) \\ 50+120+8=178 \end{gathered}`

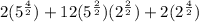
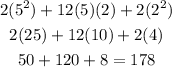
In summary, therefore, we have that:

`(\sqrt[]{5}+\sqrt[]{2})^4+(\sqrt[]{5}-\sqrt[]{2})^4=178`