Given a line of equation

To find the slope of the line above,
Finding the slope-intercept form equation of the line below,

The general form an equation of a line in the slope-intercept form below is,

The slope of the equation of the line given above is
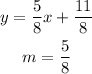
To find the slope of a line perpendicular to the equation of the line given above,
The slope of the perpendicular line is the negative reciprocal of the slope of the equation of the line given above,
The slope of the perpendicular line m₁ is,
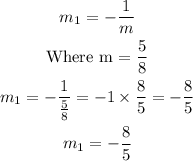
Hence, the right option is A