Question

The number of nails of a given length is normally distributed

Answer 1

Given:

The number of nails of a given length is normally distributed with a mean length of 5 in.

A standard deviation of 0.03 in.

To find:

The number of nails in a bag of 120 that are less than 4.94 in long.

Step-by-step explanation:

Using the formula,

`\begin{gathered} z=(X-\mu)/(\sigma) \\ z=(4.94-5)/(0.03) \\ z=-2 \end{gathered}`

Then the probability is,

`\begin{gathered} P(X<4.94)=P(z<-2) \\ =P(z>2) \\ =1-P(z<2) \\ =1-0.9772 \\ P(X<4.94)=0.0228 \end{gathered}`

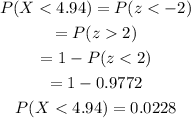
Therefore, the number of nails in a bag of 120 that are less than 4.94 in long is,

`\begin{gathered} 120*0.0228=2.736 \\ \approx3nails \end{gathered}`

So, The number of nails in a bag of 120 that are less than 4.94 in length is about 3 nails.

Final answer:

The number of nails is about 3 nails.