Question

you want to obtain a sample to estimate a population proportion. At this point in time you have no reasonable estimate for the population proportion. You would like to be 99.9% confident that you estimate is within 2.5% of the true population proportion. How large of a sample size is required?

Answer 1

We can estimate the sample size needed for a certain confidence level, admisible error and population proportion using the Cochran's formula:

`n_0=(Z^2p(1-p))/(e^2)`

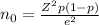
We don't have an estimation for p, the population proportion, but we will take the worst case scenario (therefore, the sample size will cover if the proportion is different), that is p=0.5.

This value of p will give us the maximum value for p(1-p) and therefore a sample size that will cover all the possible values of p.

The value of Z depends on the level of confidence, that is 99.9%. Then, the value of Z can be looked up in the standard normal distribution:

`1-\alpha=0.999\longrightarrow Z=3.291`

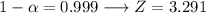
As the true proportion has to be within +/- 2.5% of the estimated proportion. the error e is 2.5%, so its value is:

`e=(2.5)/(100)=0.025`

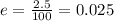
Then, we can calculate the sample size using Z=3.291, p=0.5 and e=0.025:

`\begin{gathered} n_0=(Z^2p(1-p))/(e^2) \\ n_0=((3.291)^2\cdot0.5\cdot0.5)/(0.025^2) \\ n_0\approx(10.83\cdot0.25)/(0.000625) \\ n_0\approx(2.71)/(0.000625) \\ n_0\approx4332.27 \\ n_0=4333 \end{gathered}`

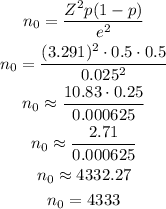
Answer: n=4,333.

The sample size has to be at least 4,333 to have a 99.9% confidence that the estimation will be within +/- 2.5% of the true population.