Question

Find the measure of the arc or angle indicated. Assume that lines which appeartangent are tangent.Find m2 KIL7x - 10СMJL7x-2K8x - 6Measure of Angle KJL =degrees

Answer 1

From the figure, the following are given:

Arc KL = 8x - 6

Arc MC = 7x - 10

∠KJL = 7x - 2

To be able to find the measure of ∠KJL, let's first determine the value of x. We will be using the following equation for Arc Length and Angles:

`\angle KJL\text{ = }(1)/(2)(Arc\text{ KL + Arc MC})`

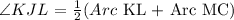
We get,

`7x-2\text{ = }(1)/(2)(8x-6\text{ + 7x - 10})`
`7x-2\text{ = }(1)/(2)(15x-16)`
`(2)(7x-2)\text{ = }(15x-16)`
`14x-4\text{ = }15x-16`
`16-4\text{ = }15x-\text{ 14x}`
`\text{ 12}^(\circ)\text{ = x}`

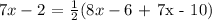
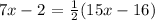
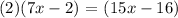
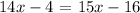
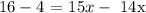
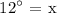
Let's determine the measure of ∠KJL.

∠KJL = 7x - 2

= 7(12) - 2

= 84 - 2

∠KJL = 82°

Therefore, the measure of ∠KJL is 82°