Question

Given the preimage and image, find the dilation scale factor. Use the forward slash

Answer 1

We are asked to determine the scale factor of th given figure. To do that we will determine the quotient between two sides of the triangle. Taking the side AB and the corresponding image we need to determine:

`SF=(A^(\prime)B^(\prime))/(AB)`

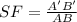
We determine the length of each of the segments using the euclidean distance formula:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

For segment A'B' we have the following end-points

`\begin{gathered} A^(\prime)=(-2,4) \\ B^(\prime)=(4,2) \end{gathered}`

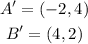
Replacing in the formula for the distance we get:

`d(A^(\prime)B^(\prime))=\sqrt[]{(4-(-2))^2+(2-4)^2}`

Solving the operations:

`\begin{gathered} d(A^(\prime)B^(\prime))=\sqrt[]{(6^2)+(-2)^2} \\ d(A^(\prime)B^(\prime))=\sqrt[]{36+4} \\ d(A^(\prime)B^(\prime))=2\sqrt[]{10} \end{gathered}`

For segment AB we have the following point:

`\begin{gathered} A=(-1,2) \\ B=(2,1) \end{gathered}`

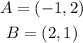
Replacing we get:

`d(AB)=\sqrt[]{(2-(-1))^2+(1-2)^2}`

Solving the operations:

`\begin{gathered} d(AB)=\sqrt[]{(3)^2+(-1)^2} \\ d(AB)=\sqrt[]{9+1} \\ d(AB)=\sqrt[]{10} \end{gathered}`

Replacing in the formula form the scale factor

`SF=\frac{2\sqrt[]{10}}{\sqrt[]{10}}=2`

Therefore, the scale factor is 2.