Answer:
x = 4
Step-by-step explanation:
Intersecting tangent- secant theorem says that if we have
then
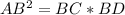
Now in our case,
AB = 8, BC = x, and CD = 12 + x; therefore, the above formula gives

Expanding the above gives
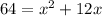
subtracting 64 from both sides gives

Using the quadratic formula, the two solutions we get are:
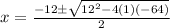
which we evaluate to get:
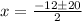
which gives us two solutions:
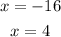
Since a length cannot be a negative number, x = 4 is our relevant solution.