Question

to keep computer files secure, many programs require the user to enter a password. The shortest allowable passwords are typically six characters long and can contain both numbers and letters. How many 6 character password are possible if A:characters can be repeatedB:characters cannot be repeated

Answer 1

`\begin{gathered} A)2176782336 \\ B)1402410240 \end{gathered}`

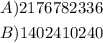
Step-by-step explanation

A) We want to find how many 6 character passwords are possible if characters can be repeated.

There are 26 letters of the alphabet and 10 numeric digits (0 - 9).

This means that each number slot has 36 choices that can be made.

Therefore, if the characters can be repeated, it means that the number of 6 character passwords possible is:

`\begin{gathered} 36^6 \\ \Rightarrow2176782336 \end{gathered}`

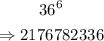
B) There are still 36 choices possible but this time there will not be any repetition.

To find the number of possible 6 character passwords, we apply the permutation formula:

`^nP_r=(n!)/((n-r)!)`

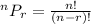
Therefore, we have:

`\begin{gathered} ^(36)P_6=(36!)/((36-6)!)=(36!)/(30!) \\ \Rightarrow(36\cdot35\cdot34\cdot33\cdot32\cdot31\cdot30!)/(30!) \\ \Rightarrow36\cdot35\cdot34\cdot33\cdot32\cdot31 \\ \Rightarrow1402410240 \end{gathered}`

That is the answer.