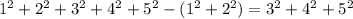Question

Im getting lost trying to solve this, could you help clarify

Answer 1

The rule for the sum of integers elevated to the second power is the following:

`\sum ^n_(k\mathop=1)k^2=(n(n+1)(2n+1))/(6)`

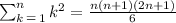
The series given can be divided in the following way:

`\sum ^(25)_(k\mathop=5)k^2=\sum ^(25)_(k\mathop=1)k^2-\sum ^4_(k\mathop=1)k^2`

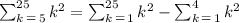
That is, to the sum of the number of k squared from 1 to 25 we subtract the sum of the numbers of k squared from 1 to 4. Now we can use the rule for the sum of integers to find each sum.

`\sum ^(25)_(k\mathop=1)k^2=(25(25+1)(2(25)+1))/(6)`

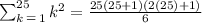
Solving the operations:

`\sum ^(25)_(k\mathop=1)k^2=5525`

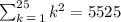
Using the formula for the next sum:

`\sum ^4_(k\mathop=1)k^2=(4(4+1)(2(4)+1))/(6)`

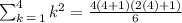
Solving the operations:

`\sum ^4_(k\mathop=1)k^2=30`

Replacing in the formula for the given sum, we get:

`\sum ^(25)_(k\mathop=5)k^2=5525-30=5495`

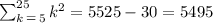
If we were asked for the sum from 3 to 5, we could do the following:

`1^2+2^2+3^2+4^2+5^2-(1^2+2^2)=3^2+4^2+5^2`