It is required to find the value of y from the given figure of circle P.
Recall that the measure of an intercepted arc is equal to the measure of the central angle.
From the circle P, notice that the measure of the central angle is 3x+7, and the measure of the intercepted arc is 5x-55.
It then follows that:

Solve the equation for x:
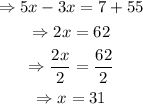
Recall the Measure of an Inscribed Angle Theorem:
The inscribed angle in the circle is ∠BAC and the intercepted arc is arc BC.
The following equation follows by the measure of an inscribed angle theorem:
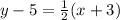
Substitute x=31 into the equation:

Solve for y:
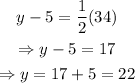
The value of y is 22.