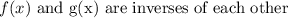Question

For each pun of functions f and g below, find f (g(x)) and g(f(x)).Then, determine whether fand g are inverses of each other.Simplify your answers as much as possible.(Assume that your expressions are defined for all x in the domain of the composition.You do not have to indicate the domain.)

Answer 1

We want to figure out if f(x) and g(x) are inverses of each other.

`f(x)=3x\text{ and }g(x)=(x)/(3)`

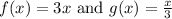
We have to find f(g(x)) and g(f(x)).

`f(g(x))=3((x)/(3))=x`

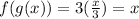
And;

`g(f(x))=((3x))/(3)=x`

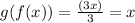
Now, since ;

`f(g(x))=g(f(x))`

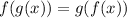
We can conclude that;

`f(x)\text{ and g(x) are inverses of each other}`

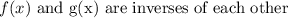
b.

`f(x)=2x+3\text{ and }g(x)=(x-3)/(2)`

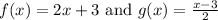
Let us compute f(g(x)) and g(f(x)) to see if these two functions are inverses of each other.

`\begin{gathered} f(g(x))=2((x-3)/(2))+3=x-3+3 \\ f(g(x))=x \end{gathered}`

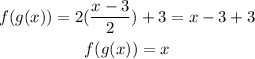
And;

`\begin{gathered} g(f(x))=(2x+3-3)/(2)=(2x)/(2) \\ g(f(x))=x \end{gathered}`

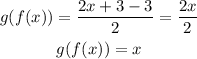
Now, since ;

`f(g(x))=g(f(x))`

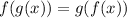
We can conclude that;

`f(x)\text{ and g(x) are inverses of each other}`