Question

Solve the polynomial equation by factoring and then using the zero product principle

Answer 1

Given;

`x^3+2x^2=16x+32`

To find: The equation in factored form and solution set.

Step-by-step explanation:

Given equation can be written as

`x^3+2x^2-16x-32=0`
`\begin{gathered} \text{When x=-2, The equation becomes,} \\ -8+8+32-32=0 \\ 0=0 \\ \text{Then (x+2) is a factor of given equation.} \end{gathered}`

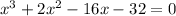
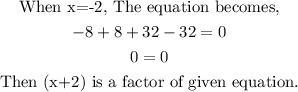
By using the factor (x+2), We proceed with the synthetic division

`\begin{gathered} x^3+2x^2-16x-32=0 \\ (x+2)(x^2-16)=0 \\ (x+2)(x^2-4^2)=0 \\ (x+2)(x+4)(x-4)=0 \end{gathered}`

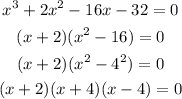
Therefore, the equation is factored form:

`(x+2)(x+4)(x-4)=0`

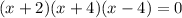
Then the solution set is

`\mleft\lbrace-2,-4,4\mright\rbrace`