Question

a.Use the Factor Theorem to find all the zeros of f(x) = 23 – 3x2 - 18x + 40 given that (x - 5) is a factor. Enter allthe zeros as a comma separated list.• Zeros:help (numbers)

Answer 1

we have the function

f(x)=x^3-3x^2-18x+40

Remember that

If (x-5) is a factor

then

when dividing f(x) by (x-5) the remainder is equal to zero

so

x^3-3x^2-18x+40 : (x-5)

x^2+2x-8

-x^3+5x^2

-------------------------

2x^2-18x+40

-2x^2+10x

-----------------

-8x+40

+8x-40

-------------

0

therefore

x^3-3x^2-18x+40=(x-5)(x^2+2x-8)

solve the quadratic equation

using the formula

a=1

b=2

c=-8

substitute given values

`x=\frac{-2\pm\sqrt[\square]{2^2-4(1)(-8)}}{2(1)}`
`x=(-2\pm6)/(2)`

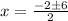
the values of x are

x=2 and x=-4

therefore

x^3-3x^2-18x+40=(x-5)(x-2)(x+4)

the answer is

the zeros are

x=-4,2,5