Question

Yea I can do tomorrow it would take me to get the money back to you

Answer 1

Given, the equation that represents the height of an object:

`y(t)=100t-16t^2`

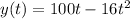
First, we will find the velocity of the object which is the first derivative of the height using the method of the limits

`(dy)/(dt)=\lim_(h\to a)(y(3+h)-y(3))/((3+h)-(3))`

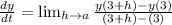
We will find the value of the function y(t) when t = 3, and when t = 3+h

`\begin{gathered} y(3+h)=100(3+h)-16(3+h)^2 \\ y(3+h)=300+300h-16(9+6h+h^2) \\ y(3+h)=300+300h-144-96h-16h^2 \\ y(3+h)=156+4h-16h^2 \\ y(3)=100(3)-16(3)^2=156 \end{gathered}`

Substitute y(3+h) and y(3) into the expression of the limit

`\begin{gathered} (dy)/(dt)|_(t=3)=\lim_(h\to a)(156+4h-16h^2-156)/(3+h-3)=\lim_(h\to a)(4h-16h^2)/(h) \\ \\ (dy)/(dt)|_(t=3)=\lim_(h\to a)(4-16h) \end{gathered}`

Where a = 0

d) compute the instantaneous velocity at t = 3

`(dy)/(dt)|_(t=3)=100-16*2*3=4`

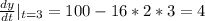
So, the answer will be:

`\begin{gathered} (dy)/(dt)|_(t=3)=\lim_(h\to a)(4-16h) \\ a=0 \\ \\ (dy)/(dt)|_(t=3)=4\text{ ft/sec} \end{gathered}`