Answer
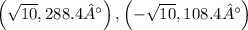
Step-by-step explanation
The polar coordinates can be represented as (r, θ).
Where;
r = √(x² + y²) and θ = tan⁻¹ (y/x)
Hence, the polar coordinates that represent the same point as the rectangular coordinate (1, -3) are calculated below:
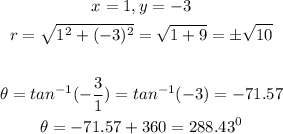
So the answers that apply are:
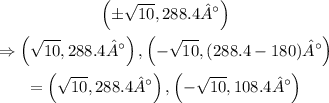
The second and the last options apply.