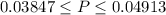So we need to build a confidence interval for the percentage of cell phone users who develop cancer of the brain or nervous system. Using P for this value we have that the confidence interval is given by:
![p-Z_{(1-(\alpha)/(2))}\cdot\sqrt[]{(p(1-p))/(n)}\leq P\leq p+Z_{(1-(\alpha)/(2))}\cdot\sqrt[]{(p(1-p))/(n)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/jwacwhbvidwxn3pbdgrxbk68vgrcv1hhft.png)
Where P is the percentage we want to estimate, p is the rate of cancer found in previous studies (0.0438%/100 in this case) and n is study sample size (here is 420079). The parameter alpha is given by the following equation:
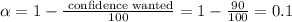
Then we have to find the Z value that is giving in tables. Since we have:
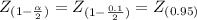
we must look for the value 0.95 in the table:
Which basically means that Z=1.65. Now let's substitute all of the values we get in the equation:
![\begin{gathered} 0.000438-1.65\cdot\sqrt[]{(0.000438(1-0.000438))/(420079)}\leq P\leq0.000438+1.65\cdot\sqrt[]{(0.000438(1-0.000438))/(420079)} \\ 0.000438-5.327\cdot10^(-5)\leq P\leq0.000438+5.327\cdot10^(-5) \\ 0.0003847\leq P\leq0.0004913 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/dday3t3zierw0lbbqq9p219ibx5mfnjnib.png)
This interval written with percentages is: