Given:
Current of the river = 4 miles per hour
Distance the boat travelled = 16 miles
Time = 3 hours
Let's find the speed of the boat.
Let x represent the speed of the boat.
Thus, we have:
Speed of boat upstream = x - 4
Speed of boat downstream = x + 4
Apply the distance formula:

Thus, we have:
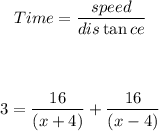
Let's solve for x:
Multiply all terms by (x+4)(x-4)
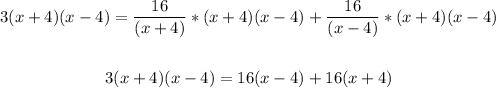
Solving further:
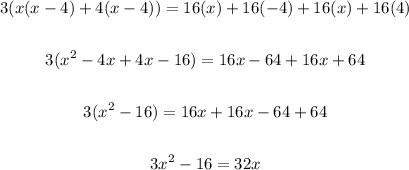
Equate to zero: