In order to solve tthis problem we must apply the "tangent quadrilateral theorem" for inscribed circles.
The theorem states the following:

In our case we have:
From the question we see that 7.4 is the radius of the circle. So the sides of the quadrilateral are:
CF = 13
FE = 12.1
ED = 7.4 + 14 = 21.4
CD = 7.4 + x
As we see, we don't know the value of x. But we can apply the "tangent quadrilateral theorem" for inscribed circles.
Which says in this case that:
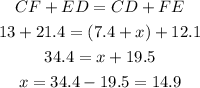
Now we can calculate the perimeter of CDEF summing the sides:
![\text{CDEF}=CD+ED+FE+CF=(7.4+14.9)+21.4+12.1+13=68.8]()