Question

At noon (t=0), two runners start running along the straight road in the same direction. The runner's speeds are v1(t)= 4/(t+1)^3, v2(t)=2/(t+1)^3 (decreasing because of fatigue). The initial distance at t=0 between runners is d= 1mine, where the fast runner is behind the slow one. Time is measured in hours make a graph of runners distance as a function of time. When do they meet?

Answer 1

From the problem, there are two running speeds :

`v_1(t)=(4)/((t+1)^3)\quad \text{and}\quad v_2(t)=(2)/((t+1)^3)`

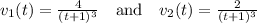
In order to graph distance vs time, we need to get the distance function first by taking the integral of both speed functions.

`d(t)=\int v(t)`

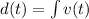
This will be :

`\begin{gathered} d_1(t)=\int v_1(t)=\int (4)/((t+1)^3)=-(2)/((t+1)^2)+C \\ d_2(t)=\int v_2(t)=\int (2)/((t+1)^3)=-(1)/((t+1)^2)+C \end{gathered}`

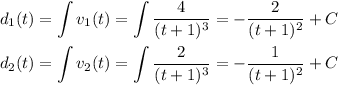
Note that the first runner is faster than the second runner, so he will be at distance 0.

and the second runner will be at distance 1.

Set t = 0 and d(t) = 0 for the first runner :

`\begin{gathered} d_1(t)=-(2)/((t+1)^2)+C \\ 0=-(2)/((0+1)^2)+C \\ 0=-2+C \\ C=2 \end{gathered}`

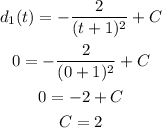
So the distance function of the first runner is :

`d_1(t)=-(2)/((t+1)^2)+2`

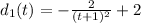
Set t = 0 and d(t) = 1 for the second runner :

`\begin{gathered} d_2(t)=-(1)/((t+1)^2)+C \\ 1=-(1)/((0+1)^2)+C \\ 1=-1+C \\ C=2 \end{gathered}`

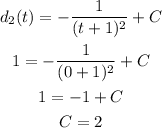
The distance function of the second runner is :

`d_2(t)=-(1)/((t+1)^2)+2`

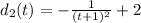
Now graph these functions :

Get atleast 3 points to graph the functions.

With t = 1, 2 and 3

For the first runner :

`\begin{gathered} d_1(t)=-(2)/((t+1)^2)+2 \\ d_1(1)=-(2)/((1+1)^2)+2=(3)/(2)\quad or\quad 1.5 \\ d_2(2)=-(2)/((2+1)^2)+2=(16)/(9)\quad or\quad 1.78 \\ d_3(3)=-(2)/((3+1)^2)+2=(15)/(8)\quad or\quad 1.875 \end{gathered}`

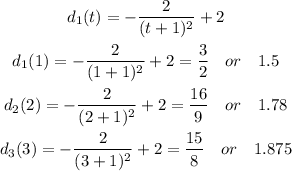
We have the points (0, 0), (1, 1.5), (2, 1.78) and (3, 1.875)

The graph will be :

where x-axis refers to the time in hours and the y-axis refers to the distance.

For the second runner :

`\begin{gathered} d_2(t)=-(1)/((t+1)^2)+2 \\ d_2(1)=-(1)/((1+1)^2)+2=(7)/(4)\quad or\quad 1.75 \\ d_2(2)=-(1)/((2+1)^2)+2=(17)/(9)\quad or\quad 1.89 \\ d_2(3)=-(1)/((3+1)^2)+2=(31)/(16)\quad or\quad 1.94 \end{gathered}`

We have the points (0, 1), (1, 1.75), (2, 1.89) and (3, 1.94)

The graph will be :

The blue curve is for the first runner and the orange curve is for the second runner.

To get the point where the two runners will meet. the distance must be equal or the y-coordinate must be the same.

Equating both distance functions :

`\begin{gathered} d_1(t)=d_2(t) \\ -(2)/((t+1)^2)+2=-(1)/((t+1)^2)+2 \\ -(2)/((t+1)^2)=-(1)/((t+1)^2) \\ -2(t+1)^2=-(t+1)^2 \\ -2(t+1)^2+(t+1)^2=0 \\ -(t+1)^2=0 \\ (t+1)^2=0 \\ t=-1 \end{gathered}`

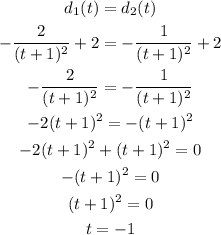
Since the time is negative, they will not meet each other. and their speed will not be equal to zero.

Looking at the graph, the horizontal asymptote is at y = 2, which they will never reach.