Question

Find the distance between each pair of parallel lines with the given equation Y=1/3x +2 and y=1/3x-8

Answer 1

When the equations of two parallel lines are given in slope-intercept form, as:

`\begin{gathered} y=mx+b_1 \\ y=mx+b_2 \end{gathered}`

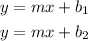
The distance between those two lines is given by the formula:

`d=\fracb_1-b_2{\sqrt[]{1+m^2}}`

For the given equations:

`\begin{gathered} y=(1)/(3)x+2 \\ y=(1)/(3)x-8 \end{gathered}`

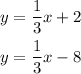
We can see that m=1/3, b₁=2 and b₂=-8. Then, the distance between those two lines, is:

`\begin{gathered} d=\frac2-(-8){\sqrt[]{1+((1)/(3))^2}} \\ =\frac2+8{\sqrt[]{1+(1)/(9)}} \\ =\frac{10}{\sqrt[]{(10)/(9)}} \\ =10\cdot\sqrt[]{(9)/(10)} \\ =\frac{\sqrt[]{10^2}}{\sqrt[]{10}}\cdot\sqrt[]{9} \\ =\sqrt[]{(10^2)/(10)}*3 \\ =\sqrt[]{10}*3 \\ =3\cdot\sqrt[]{10} \\ \approx9.487\ldots \end{gathered}`

Therefore, the distance between those two lines is:

`3\cdot\sqrt[]{10}`