Question

I’m having a hard time solving this it is from my ACT prep guide

Answer 1

Given the initial expression

`\sin ^(-1)(-\frac{\sqrt[]{3}}{2})`

Set

`\begin{gathered} \sin ^(-1)(-\frac{\sqrt[]{3}}{2})=x \\ \Rightarrow\sin x=-\frac{\sqrt[]{3}}{2} \end{gathered}`

On the plane, using the unitary circle

Furthermore,

`\begin{gathered} \sin x=(O)/(H) \\ \Rightarrow(O)/(H)=-\frac{\sqrt[]{3}}{2}=\frac{-\frac{\sqrt[]{3}}{2}}{1} \end{gathered}`

This is a well-known triangle,

Therefore, the answer is

`\Rightarrow x=-(\pi)/(3)`

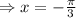
x=-pi/3 is the answer (notice that it corresponds to the blue angle in the first figure)

Remember that the domain of arcsin(x) is [-pi/2,pi/2]