a) The distance between two points is determined following the next formula:
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
You have the points:
P1 ( 9 , 2 ) X1=9 Y1=2
P2 ( - 4 , 3 ) X2=-4 Y2=3
Then the distance is:
![d=\sqrt[]{(-4-9)^2+(3-2)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/b9kb5nks56crku58ed5nyq65zg8ri7ipsw.png)
![d=\sqrt[]{(-13)^2+1^2}](https://img.qammunity.org/2023/formulas/mathematics/college/5sp3oqox3nn7hqf2k3cn2b7vt7p45i0u81.png)
![d=\sqrt[]{169+1}=\sqrt[]{170}=13.03](https://img.qammunity.org/2023/formulas/mathematics/college/i2s518x0z5a09n85crertqnw1huzpf32xq.png) The distance between the two points is 13.03 units.
The distance between the two points is 13.03 units.The coordinate of the midpoint is calculated following the next formula:
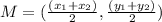
Then the midpoint will have the coordinates:
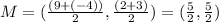 The midpoint is M= (5/2 , 5/2)
The midpoint is M= (5/2 , 5/2)--------------------------------------
b) the slope(m) can be found using two points with the next formula:
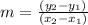
Then the slope will be:
P1 ( - 2 , - 9 )
P2 ( 1 , 6 )
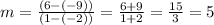 The slope is m=5
The slope is m=5