Question

Find the inverse of the function below and graph of both the function and is inverse on the same coordinate plane.

Answer 1

Let's start finding the inverse of the function by changing f(x) to y:

`y=x^2+2`

We then interchange x and y, getting:

`x=y^2+2`

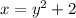
We now solve for y.

`\begin{gathered} y^2=x-2 \\ y=\sqrt[]{x-2} \end{gathered}`

Hence, the inverse of the function f(x) = x^2 + 2 is:

`f^(-1)(x)=\pm\sqrt[]{x-2}`

Since we are only considering the domain x >= 0, we will only consider the inverse of the function that is positive, that is:

`f^(-1)(x)=\sqrt[]{x-2}`

The plot of the function and its inverse is shown in the figure above.