Question

I need help to see if my daughter has the right answer

Answer 1

Step-by-step explanation

We need to find the zeros of the following function:

`g(x)=-x^3+x^2+12x`

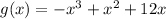
First of all it's important to note that all the terms have a power of x i.e. there's no constant term. This means that x=0 is a zero of the function:

`g(0)=-0^3+0^2+12\cdot0=0+0+0=0`

So we have our first zero. Then you can notice that x is a common factor to all terms so we can rewrite our function:

`\begin{gathered} g(x)=-x^3+x^2+12x=-x^2\cdot x+x\cdot x+12\cdot x=(-x^2+x+12)\cdot x \\ g(x)=(-x^2+x+12)\cdot x \end{gathered}`

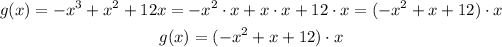
So we can write g(x) as a product of two expressions. This means that if one of the expression is 0 for a given x then g(x) is also 0 for that x. Then the zeros of each term are also the zeros of g(x). The left term is just x and its zero is x=0 the one that we already found. Then the remaining zeros of g(x) are the x-values that make the quadratic expression on the left equal to 0:

`-x^2+x+12=0`

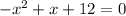
Remember that for a quadratic equation ax²+bx+c=0 its zeros are given by the following formula:

`r=(-b\pm√(b^2-4ac))/(2a)`

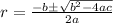
In this case we have a=-1, b=1 and c=12 so the zeros of the quadratic expression are:

`r=(-1\pm√(1^2-4\cdot(-1)\cdot12))/(2\cdot(-1))=(-1\pm√(49))/(-2)=(-1\pm7)/(-2)`

Then we have another two zeros:

`\begin{gathered} r=(-1+7)/(-2)=(6)/(-2)=-3 \\ r=(-1-7)/(-2)=-(8)/(-2)=4 \end{gathered}`

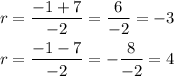
Then the three zeros of g(x) are x=0, x=-3 and x=4.

In a graph the zeros are the x-values of the points where the graph intercepts the x-axis so the answer is the function that intercepts the x-axis at -3, 0 and 4.

Answer

Then the answer is option A.